Types Of Physical Quantities With Examples

Rate this post

Understanding the “Types of Physical Quantities with Examples” is essential for anyone preparing for competitive exams. It is a significant aspect of physics within the realm of general science, and this knowledge encompasses a range of important concepts that are widely applicable in various competitive examinations.

In the world of science and physics, physical quantities play a crucial role in understanding the natural world and describing the fundamental properties of matter and energy. These quantities are essential building blocks for formulating scientific theories, making predictions, and unravelling the mysteries of the universe.

Table of Contents

What are Physical Quantities?

In the world of physics, a physical quantity refers to a measurable attribute of a material or system that can be expressed through measurement.

It is represented by a numerical value multiplied by a specific unit of measurement. For instance, consider the mass (symbolized by ‘m’), which can be quantified as m=n kg, with ‘n’ being the numerical value and ‘kg’ representing the unit (kilogram).

These physical quantities play a crucial role in understanding and describing the behaviour of objects and phenomena in the natural world.

They form the building blocks for scientific equations, enabling us to make predictions and gain insights into the fundamental laws of nature.

In summary, physical quantities provide the means to quantify and analyze various properties of physical systems, allowing us to delve deeper into the universe’s complexities.

Types of Physical Quantities

Based on Units and their Measurement

▪ Based on units and their measurement, there are three types of physical quantities: Fundamental and Derived, and Supplementary Physical Quantities.

Fundamental or Basic Physical Quantities

▪ Fundamental physical quantities are the basic and essential measurable properties in physics that are the building blocks for all other derived physical quantities.

▪ They are independent and cannot be defined in terms of other physical quantities. In most scientific systems of measurement, there are typically a set of fundamental physical quantities, from which all other quantities can be derived.

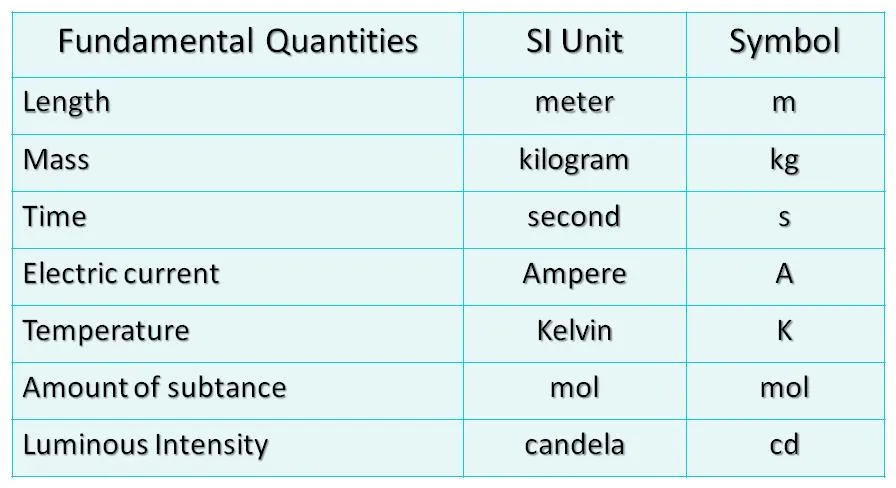
▪ These cannot be defined in terms of other physical quantities. The seven fundamental physical quantities in the International System of Units (SI) are:

Length (meter, m): Measures the extent or magnitude of a space or distance.
Mass (kilogram, kg): Represents the amount of matter in an object.
Time (second, s): Measures the duration or interval between events.
Electric Current (ampere, A): Describes the flow of electric charge through a conductor.
Thermodynamic Temperature (Kelvin, K): Indicates a system’s heat or coldness level.
Amount of Substance (mole, mol): Measures the number of particles (atoms, molecules, etc.) in a substance.
Luminous Intensity (candela, cd): Quantifies the intensity of visible light emitted in a specific direction.

✅ Read Also: Image formed by Plane Mirror

▪ These fundamental physical quantities form the foundation of physics and are essential for expressing and understanding various phenomena and laws governing the natural world.

▪ Other physical quantities, known as derived quantities, are derived from combinations of these fundamental quantities through mathematical equations.

Derived Physical Quantities

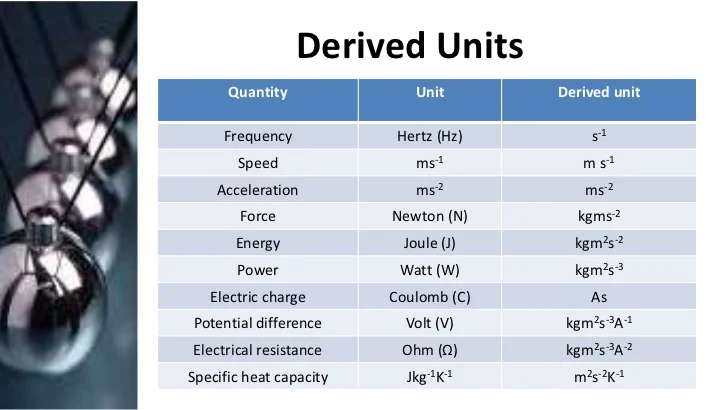
▪ Derived physical quantities are measurable properties in physics that are derived from combinations of fundamental physical quantities.

▪ Unlike fundamental quantities, which are independent and cannot be defined in terms of other physical quantities, derived quantities are expressed as mathematical combinations or ratios of fundamental quantities.

▪ In the International System of Units (SI), derived physical quantities are numerous and cover a wide range of phenomena. Some common examples of derived physical quantities include:

Speed (meter per second, m/s): Derived from dividing distance (length) by time.
Area (square meter, m²): Derived from multiplying the length by width.
Volume (cubic meter, m³): Derived from the three-dimensional measure of space.
Acceleration (meter per second squared, m/s²): Derived from the change in velocity divided by time.
Force (Newton, N): Derived from mass multiplied by acceleration.
Energy (joule, J): Derived from force multiplied by distance.
Power (watt, W): Derived from energy divided by time.
Pressure (Pascal, Pa): Derived from force per unit area.
Electric Charge (coulomb, C): Derived from electric current multiplied by time.
Voltage (volt, V): Derived from electric energy per unit charge.

▪These derived physical quantities are vital in physics and various other sciences, as they allow us to describe and quantify complex phenomena and relationships in a concise and consistent manner.

▪ By combining fundamental quantities into derived quantities, scientists can better analyze and understand the behaviour of objects and systems in the natural world.

Here is a table that summarizes the two types of physical quantities:

Type	Description	Examples
Fundamental	Cannot be defined in terms of other physical quantities	Length, mass, time, electric current, temperature, amount of substance, luminous intensity
Derived	Can be defined in terms of fundamental physical quantities	Speed, force, energy, power, pressure, volume, density

Derived Physical Quantities (Photo: Slideshare)

Supplementary Physical Quantities

Supplementary quantities are dimensionless, which means that they do not have any dimensions. This means they cannot be added, subtracted, multiplied, or divided by other physical quantities. However, they can be used to create derived units.

The radian is the unit of plane angle. It is defined as the angle subtended by an arc of a circle that is equal in length to the radius of the circle.

The steradian is the unit of solid angle. It is defined as the angle subtended by a unit sphere at a point on its surface.

Supplementary quantities are important because they are used to measure physical quantities that are not directly measurable in terms of the seven fundamental quantities.

For example, the plane angle measures the size of an angle, and the solid angle measures the amount of space enclosed by a surface.

There are two supplementary quantities:

Plane angle (radian, rad)
Solid angle (steradian, sr)

Here is a table that summarizes the three types of physical quantities:

Type	Description	Examples
Fundamental	Cannot be defined in terms of other physical quantities	Length, mass, time, electric current, temperature, amount of substance, luminous intensity
Derived	Can be defined in terms of fundamental physical quantities	Speed, force, energy, power, pressure, volume, density
Supplementary	A special type of derived physical quantity	Plane angle (measured in radians)

Based on Direction and Magnitude

Based on direction and Magnitude, there are two types of physical quantities: Scalar and Vector Quantity

Scalar Quantity

A scalar quantity is a type of physical quantity in physics that is described solely by its magnitude or numerical value. In other words, scalar quantities do not have a direction associated with them, and a single real number fully characterizes them.

Scalar quantities are expressed using units of measurement and can be added, subtracted, multiplied, and divided algebraically.

Examples of scalar quantities include:

Mass (kg): The amount of matter in an object.
Temperature (°C or K): A measure of the average kinetic energy of particles in a substance.
Time (s): The duration or interval between events.
Distance (m): The extent of space between two points.
Speed (m/s): The rate at which an object covers distance.
Energy (Joule, J): The capacity to work or transfer heat.

When dealing with scalar quantities, the mathematical operations are straightforward, as they involve only manipulating numerical values and units without considering direction.

For instance, adding two scalar quantities, like 5 kg and 3 kg, is simply 8 kg, without any vector-like considerations.

Scalar quantities are fundamental in many aspects of physics and play a significant role in various calculations and equations.

Vector Quantity

A vector quantity is a type of physical quantity in physics that requires both magnitude and direction to describe it fully.

In contrast to scalar quantities, which are characterized solely by their magnitude, vector quantities involve both numerical values and specified directions.

Vectors are represented graphically by arrows, the length of which corresponds to the vector’s magnitude, and the arrow’s direction represents the vector’s direction.

In physics, vectors are commonly used to describe quantities with both magnitude and direction, particularly in studying motion, forces, and other phenomena involving spatial relationships.

Mathematical operations involving vectors, such as addition, subtraction, and dot products, consider both magnitude and direction.

Vectors are essential in various scientific and engineering applications, enabling us to analyze and predict complex behaviours and interactions in the natural world.

Examples of vector quantities include:

Displacement (m): The change in position of an object in a specific direction.

Velocity (m/s): The rate of change of displacement with respect to time, including direction.

Acceleration (m/s²): The rate of change of velocity with respect to time and its direction.

Force (Newton, N): A push or pull on an object, characterized by magnitude and direction.

Momentum (kg·m/s): The product of an object’s mass and velocity, including direction.

Electric and Magnetic Fields (N/C, T): Vectors that indicate the direction and strength of electric and magnetic forces at various points in space.

Frequently Asked Questions (FAQs)

Q1. What are the 3 types of physical quantities?

Based on Units and Measurements Physical quantities are classified into three types. These are :
Fundamental quantities.
Derived quantities.
Supplementary quantities.

Q2. What are the two types of physical quantity based on direction and magnitude?

All physical quantities are classified into vectors and scalars based on direction and magnitude.

Q3. What is derived physical quantity?

Derived physical quantities can be derived from two or more fundamental physical quantities. Area, speed, volume, force, etc. are examples of derived quantities.

Q4. What are the 7 fundamental physical quantities defined?

The present SI has 7 base quantities: time, length, mass, electric current, thermodynamic temperature, amount of substance, and luminous intensity.

Q5. What is a fundamental quantity?

The physical quantities that do not depend on other physical quantities for their measurements are known as fundamental or basic quantities.

Q6. What are basic physical quantities?

There are 7 fundamental quantities, these are:
1. Length
2. Mass
3. Time
4. Temperature
5. Amount of a Substance
6. Current
7. Luminous intensity

Types of Physical Quantities with Examples: General Science Physics

What are Physical Quantities?